June 16, 2023
Defining an $N_{\infty}$-operad using transfer systems
This time, we want a combinatorial understanding of $N_{\infty}$-operads in a suitable $G$-equivariant setting. The goal is establishing, for $G=C_{p^n}$, a one-one correspondence between the natural order on the collection of $N_{\infty}$-operads and the poset structure of Stasheff’s $(n+1)$-associahedron, $\mathcal{A}_{n+1}$. This is work by Balchin-Barnes-Roitzheim[1].
Instead of the traditional way, as mentioned right at the article’s outset, we want to understand $N_{\infty}$-operads differently in a combinatorial way. The key player is the following result that was conjectured by Blumberg-Hill [2] and proved by a series of works by Bonventre-Pereira, Gutiérrez-White, and Rubin independently. I just state the result by getting into the details of the proof
$\mathbf{Thm} \ 1.1. \ $
\[\text{Ho}\left(N_{\infty}\text{-op} \right) \xrightarrow{\sim} \mathfrak{Ind}\]where $N_{\infty}\text{-op}$ is the category of $N_{\infty}$-operads, and $\mathfrak{Ind}$ is the category of indexing systems with poset structure.
Now we’ll see what indexing systems are next.
For that, they’re some machinery that we introduce first.
$\mathbf{Def} \ 1.2. \ $ A categorical coefficient system is a contravariant functor
\[\underline{\mathcal{C}} : \text{Orb}_{G} \rightarrow \mathcal{Cat}\]from the orbit category of $G$ to the category of small categories.
Typically, there’s an abuse of notation by omitting the word categorical.
We have the notion of a symmetric monoidal coefficient system, which is a contravariant functor from the orbit category of $G$ to the category of symmetric monoidal categories and strong symmetric monoidal functors.
The category of interest for us is the coefficient system of finite G-sets.
$\mathbf{Def} \ 1.3. \ $ Suppose $\underline{\mathcal{Set}}$ is the symmetric monoidal coefficient system of finite sets, with $\underline{\mathcal{Set}}(H) = \mathcal{Set}^{H}$. The symmetric monoidal operation is the disjoint union.
Now the idea is to associate to every $N_{\infty}$-operad a sub coefficient system of $\underline{\mathcal{Set}}$.
Next is the definition of an indexing system using all the machinery we’ve introduced.
$\mathbf{Def} \ 1.4. \ $ An indexing system is a sub symmetric monoidal coefficient system that’s closed under subobjects and self-induction.
Now the latter condition, for a full sub-symmetric monoidal coefficient system $\mathcal{Z}$, translates to the following.
\[H/H' \in \mathcal{Z}(H) \wedge K \in \mathcal{Z}(H') \Rightarrow H \times_{H'} K \in \mathcal{Z}(H)\]We now compare indexing systems to transfer systems [].
$\mathbf{Lemma} \ 1.5. \ $ An indexing system determines (and is also determined by) a set $\mathcal{Z}_{H}$ for $H \leq G$, with subgroups of $H$ satisfying the following axioms:
-
$H/H \in \mathcal{Z}(H)$
-
$H/H’ \in \mathcal{Z}(H) \Rightarrow gHg^{-1}/gH’g^{-1} \in g\mathcal{Z}g^{-1}$
-
$H/H’ \in \mathcal{Z}(H) \ \wedge \ H’/K \in \mathcal{Z}(h’) \Rightarrow H/K \in \mathcal{Z}(H)$
-
$H/H’ \in \mathcal{Z}(H) \Rightarrow K(K \cap H’) \in \mathcal{K} \ , \forall \ K \leq H$
All this data is referred to as a transfer system.
Alternatively, we have the following definition.
$\mathbf{Def} \ 1.6. \ $ For a transfer system $\mathcal{Z}(H)$ we can define a set abstractly
\[\\{ N_{H'}^{H} \mid H/H' \in \mathcal{Z}(H), H \leq G \\}\]We call these norm maps.
Using all these, now we have an alternate description of an $N_{\infty}$-operad that I state next.
$\mathbf{Cor} \ 1.7. \ $
$G$ is a finite group. An $N_{\infty}$ operad for $G$, upto homotopy is defined as the data of the set $X = \{N_{H}^{K} \mid 1 \leq K < H \leq G \}$ satisfying the following (and all conjugates thereof)
- $N_{H}^{K} \in X \ \wedge M < H \Rightarrow N_{K \cap M}^{M} \in X$ (Restriction Axiom aka $\mathfrak{RA}$)
- $N_{L}^{K} \in X \ \wedge N_{H}^{K} \in X \Rightarrow N_{L}^{H} \in X$ (Composition Axiom aka $\mathfrak{CA}$)
It’s important to note that the notation choice makes sense so that the Mackey functor of an algebra $A$ over an $N_{\infty}$-operad $\mathcal{O}$ has multiplicative norm maps $N_{K}^{H}: \pi_{0}^{K}(A) \rightarrow \pi_{0}^{H}(A)$.
The case of $G= C_{p^n}$
We now look at the case of interest, i.e. when $G= C_{p^n}$ where $p$ is a prime.
The goal is to understand the sequence $\{ \mid N_{\infty}(C_{p^n}) \mid \}$ .
The cases of $n=0$ and $n=1$ are trivial. We look at the case of $n=2$.
We start by drawing out all our possibilities and then using the axioms $\mathfrak{RA}$ and $\mathfrak{CA}$ to eliminate redundant structures.
.png)
.png)
The third structure i.e. $\{N_{0}^{1}, N_{1}^{2} \}$ isn’t an $N_{\infty}$-structure using $\mathfrak{CA}$ and the sixth and eighth structures i.e. $\{N_{0}^{2}, N_{1}^{2} \} \ , \ \{N_{0}^{2} \}$ aren’t $N_{\infty}$-structures by an application of $\mathfrak{RA}$.
Thus we can conclude that $\mid N_{\infty}(C_{p^2}) \mid = 5$
There’s a noticeable pattern that we’ve here.
We now spend some time recalling the Catalan Numbers, which obviously have been popping up so far.
The Catalan sequence is a widespread sequence popping up in various enumerations problems, two of which we’ll use directly. We first define the sequence.
$\mathbf{Def} \ 2.1. \ $ The Catalan numbers are terms of the sequence $\{ C_n \}$ defined as follows:
\[C_n = \frac{1}{n+1}\binom{2n}{n} = \frac{(2n)!}{(n+1)!n!}\]We also recall that they satisfy the following recurrence relation.
\[C_0 = 1\] \[C_{n+1} = \sum_{l=0}^{n}C_l C_{n-l} \\ , \\ n\geq 0\]Some examples of enumeration problems where Catalan numbers pop up are the following:
- $C_n =$ # rooted binary trees with $n+1$ vertices
- $C_n =$ # ways of cutting a convex polygon with $n+2$ sides into triangles
- $C_n=$ # permutations of $\{1, \cdots , n\}$ with no three terms in increasing order
BBR product
We now define an operation on $N_{\infty}$-operads that I call the Balchin-Barnes-Roitzheim (BBR) product, also called the o-dot product.
\[\odot: N_{\infty}(C_{p^k}) \times N_{\infty}(C_{p^{l}}) \rightarrow N_{\infty}(C_{p^{k+l+2}})\]For $X \in N_{\infty}(C_{p^k})$ and $X’ \in N_{\infty}(C_{p^l})$, $X \odot X’ \in N_{\infty}(C_{p^{k+l+2}})$ is defined as follows:
\[X \odot X' = X \coprod \Sigma^{k+2}X' \coprod \\{N_{k+1}^{m} \\}_{k+1 < m \leq k+k+2}\]where $\Sigma^{j}N_{a}^{b} = N_{a+j}^{b+j}$
Now there’s a pictorial way to work and see things that we see next.
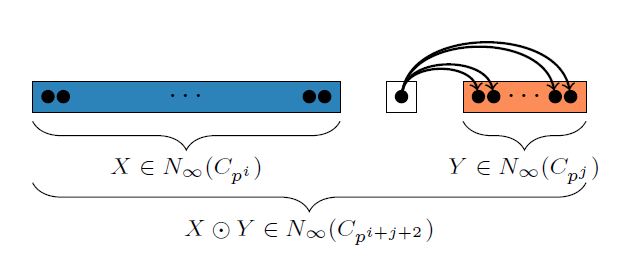 |
|---|
| Pictorial illustration of the BBR product from the BBR paper[] |
We now see an example:
Let $X,Y \in N_{\infty}(C_{p^2})$
 |
|---|
| It’s easy to see how the operation works and that it’s not commutative |
We now see the result that lets us use the BBR product for our purposes.
$\mathbf{Prop} \ 3.1. \ $ $X \in N_{\infty}(C_{p^k})$ and $Y \in N_{\infty}(C_{p^l})$. $X \odot Y$ is an object in $N_{\infty}(C_{p^{k+l+2}})$ for $k,l \geq -1$. Also conversely, if we’ve $X \odot Y \in N_{\infty}(C_{p^{k+l+2}})$ then $X$ and $Y$ are $N_{\infty}$ structures.
Now we make our next step towards computing $\mid N_{\infty}(C_{p^{n}}) \mid$
$\mathbf{Prop} \ 3.2. \ $ We have the following recurrence relation
\[|N_{\infty}(C_{p^{-1}}) | = 1\] \[|N_{\infty}(C_{p^n})| = \sum_{q=0}^{n}|N_{\infty}(C_{p^{q-1}})| |N_{\infty}(C_{p^{n-q-1}})|, \\ n \geq 0\]The idea of the proof is to use the last proposition after showing that every $X \in N_{\infty}(C_{p^n})$ can be written as $X = Y \cdot Z$ where $Y \in N_{\infty}(C_{p^{q-1}})$ and $Z \in N_{\infty}(C_{p^{n-q-1}})$
Now we begin with $j \in \mathbb{Z}$ such that it’s the minimum integer such that $N_{n}^{j}$ is in $X$. The cases of $j=0$ and $j=n$ are straightforward, with $Y = \emptyset$ and $Z = \emptyset$ in both cases.
Now if $O < j < n$, then clearly we can split off $C_{p^i}$ with $0 \leq i < j$. Let’s call this part $Y \in N_{\infty}(C_{p^{j-1}})$ and the remaining part $X’$ Now it’s easy to see that this part’s like $\emptyset \cdot Z$ for some $Z \in N_{\infty}(C_{p^{n-j-1}})$.
We can thus conclude that $X = Y \cdot Z$
Now a consequence of the previous result is the following corollary.
$\mathbf{Cor} \ 3.3. \ $
For $G= C_{p^n}$, and $X \in N_{\infty}(C_{p^n})$ we can write $X = Y \cdot Z$ for some suitable $N_{\infty}$-operads $Y$ and $Z$.
Now as a corollary to this, we have the first part of the main theorem.
$\mathbf{Cor} \ 3.4. \ $ We have a bijection
\[\\{\text{rooted binary trees with} \\ n+2 \\ \text{vertices} \\} \Leftrightarrow \\{N_{C_{p^n}} \\}\]The recursive construction works as follows:
 Then
Then
.png) Relation to Stasheff's Associahedra
------
We now define the associahedron.
For binary trees, let's define the following relation:
For binary trees $X$ and $Y$
$$X < Y \Leftrightarrow \\{ \text{Y can be obtained from}\\ X \\ \text{by means of a finite sequence of rotations} \\}$$
$\mathbf{Def} \\ 4.1. \\ $
The poset structure on binary trees with $n+1$ vertices induced by the above relation is referred to as Stasheff's $n$-associahedron $\mathcal{A}_{n}$.
We now equip $N_{\infty}$-operads for $G= C_{p^n}$ with a poset structure by defining the following order relation:
For $X, Y \in N_{\infty}(C_{p^n})$
$$X < Y \Leftrightarrow \\{ Y \\ \text{can be obtained via}\\ X \\ \text{by means of a sequence of norm map additions} \\}$$
What follows next is the main result in all its glory and completeness, which basically tells us about the agreement of the poset structures we just saw.
$\mathbf{Thm} \\ 4.2. \\ $
*We have an order-reflecting and order-preserving bijection*
$$\\{\text{rooted binary trees with} \\ n+2 \\ \text{vertices} \\} \Leftrightarrow \\{N_{C_{p^n}} \\} \Leftrightarrow \mathcal{A}_{n+1}$$
The remaining part of this result is the second bijection.
The idea is to prove the correspondence between adding a norm map to the $N_{\infty}$-operad and a clockwise rotation operation to a tree. Here's a pictorial description of the $\Leftarrow$ part of the equivalence:
Relation to Stasheff's Associahedra
------
We now define the associahedron.
For binary trees, let's define the following relation:
For binary trees $X$ and $Y$
$$X < Y \Leftrightarrow \\{ \text{Y can be obtained from}\\ X \\ \text{by means of a finite sequence of rotations} \\}$$
$\mathbf{Def} \\ 4.1. \\ $
The poset structure on binary trees with $n+1$ vertices induced by the above relation is referred to as Stasheff's $n$-associahedron $\mathcal{A}_{n}$.
We now equip $N_{\infty}$-operads for $G= C_{p^n}$ with a poset structure by defining the following order relation:
For $X, Y \in N_{\infty}(C_{p^n})$
$$X < Y \Leftrightarrow \\{ Y \\ \text{can be obtained via}\\ X \\ \text{by means of a sequence of norm map additions} \\}$$
What follows next is the main result in all its glory and completeness, which basically tells us about the agreement of the poset structures we just saw.
$\mathbf{Thm} \\ 4.2. \\ $
*We have an order-reflecting and order-preserving bijection*
$$\\{\text{rooted binary trees with} \\ n+2 \\ \text{vertices} \\} \Leftrightarrow \\{N_{C_{p^n}} \\} \Leftrightarrow \mathcal{A}_{n+1}$$
The remaining part of this result is the second bijection.
The idea is to prove the correspondence between adding a norm map to the $N_{\infty}$-operad and a clockwise rotation operation to a tree. Here's a pictorial description of the $\Leftarrow$ part of the equivalence:
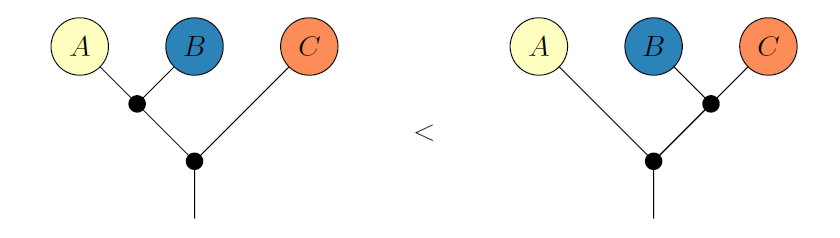 $$\Updownarrow$$
$$\Updownarrow$$
.png) The $\Rightarrow$ part's not as straightforward as this.
I don't get into all the details; it just boils down to the following 3 cases:
The $\Rightarrow$ part's not as straightforward as this.
I don't get into all the details; it just boils down to the following 3 cases:
.png) from which the first and second cases are almost immediate, while the third needs a bit of work for whose details the reader's redirected to [1].
References
------
1. Roitzheim, Constanze, Barnes, David, Balchin, Scott (2022) N-infinity operads and associahedra. Pacific Journal of Mathematics, 315 (2). pp. 285-304. E-ISSN 0030-8730. (doi:10.2140/pjm.2021.315.285) (KAR id:77048) [link](https://kar.kent.ac.uk/77048/11/Roitzheim%20published%20version.pdf)
2. Blumberg, Andrew J., and Michael A. Hill. "Operadic multiplications in equivariant spectra, norms, and transfers." Advances in Mathematics 285 (2015): 658-708. [link](https://pdf.sciencedirectassets.com/272585/1-s2.0-S0001870815X00144/1-s2.0-S000187081500256X/main.pdf?X-Amz-Security-Token=IQoJb3JpZ2luX2VjEIL%2F%2F%2F%2F%2F%2F%2F%2F%2F%2FwEaCXVzLWVhc3QtMSJHMEUCIQCO6vfKKcndrwlTgCHNSbiJ2G8VCUH%2FilkcfjXDXcyxTgIgZtDHloTThyJm1sH04X9w7nLaUBSaNozzN2P5W8cezasquwUI2%2F%2F%2F%2F%2F%2F%2F%2F%2F%2F%2FARAFGgwwNTkwMDM1NDY4NjUiDCT15dfFZPANtwdJuiqPBTyJy7Ib9n2n6I1jiycZo62hL01bwagymcPU1U5wh4Fsp6qRYZQewL3jJCPhUwiqbHKpvQ7deLPLDZuMsIfHPbegRL%2F1IOh7egNBX3lwbO8bDBkMdbgjWRecwQMpKIQV3XXZPe4nnK5BD50BkRpw2opoE3GNN%2FelGr6OYde4HT4P%2F730lgzfQyf8JlyPow8HEU4vvoph1T9iw6c346bwIdWZ%2FT%2Fcj8DEGfAXTdHI1c%2Bkd80q6Dx4i1wDWblQFRZrRU921OgPvLUF3uTONERuN85maW%2F7DdgQ3Zip3l3CXYf9cCCKNW%2B7fvHionqKcCmYGbx8p%2Ff2PzKGVssrfqZJ7MX9OZlOWpbJxrXLRNXq%2BrOZAES%2F1SafzrSagVXiI3zYMqoLTDcTjkQi6cacwGNjErZNocPbpSViguC%2FwXJAXMnOILw1BWsvTHsUgYrhspqapslU9yVhCU57dTgOHYeuS4%2BQAgc0qq%2BBAZbKrxTKP%2B08z6GT2CdAU4aJrtH6SVAvwAtqgMNoSn7MCx%2B1mQZ1wjMTMXwG3h5HfQcUT3%2BdsK6UHfiTKKKrHZrwRyUrUTN3V8ocGybVFA3iOAoMi8lWAzpYWbOXdl3ys7nDdw%2BK%2BuISeivXEzSQiQ09u7emrDA0G%2BFaAI9cOfy8vdW6QUn0jbNHrYjDpc%2BTbUoRsXjQPfs33%2FHoBNwDK03tyUkiNbYTQyskE%2FyABbmkRaSKyNx12BX8EnJic1lk6FClJy0XtBluKnqEUsF4QxSbHoyYmxL9IsYCPjwtATsL7M4eERN8XMDCF4SoAxQHCgDcKNrUnnQ3mlug5tH6jC2%2BuZzRA%2Flf8Oy6rnooeLgkCMalB%2FZYRY%2FpNV1uQfamWXuvndfbQn4wqJnSpAY6sQFMkNuESlJQl3AjJPupNwtns3qtMYKW96tb%2FWNJ4GT5RAPrH1qSVgO%2BtI%2Bvz5TmwcBPYqtOCJLMpa0cqjtbeGaTTRDnwPui7DBwWCJGJ5Qor%2ByIVbEhsaahQdGtAq6rWdQnT1Tlt6X51984kibwuU98VVPsCip9l1JNgAcDR7eM8KNcdikU3Xw9h3tVdu3J3OlXdlPE3rl%2B34WDdrtWicA%2FcKqOl2ySqo0PtMrVvtMjQRI%3D&X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Date=20230622T185116Z&X-Amz-SignedHeaders=host&X-Amz-Expires=299&X-Amz-Credential=ASIAQ3PHCVTYR47UNKXY%2F20230622%2Fus-east-1%2Fs3%2Faws4_request&X-Amz-Signature=c18e3dea7a3496c3ff156ac0be1a78f3c0444ce307595dbf4d1e548b14d38e1e&hash=d24d35890bdfe424228276c45f5dc1c2c3b21a3f7ce2c71da852cab1813cc034&host=68042c943591013ac2b2430a89b270f6af2c76d8dfd086a07176afe7c76c2c61&pii=S000187081500256X&tid=spdf-400ca13a-e793-461d-b061-5aac41cb1648&sid=92a107798e6f5344926abbd44f81c8e93754gxrqb&type=client&tsoh=d3d3LnNjaWVuY2VkaXJlY3QuY29t&ua=0c08520b065400005950&rr=7db6ae823d979a72&cc=in)
from which the first and second cases are almost immediate, while the third needs a bit of work for whose details the reader's redirected to [1].
References
------
1. Roitzheim, Constanze, Barnes, David, Balchin, Scott (2022) N-infinity operads and associahedra. Pacific Journal of Mathematics, 315 (2). pp. 285-304. E-ISSN 0030-8730. (doi:10.2140/pjm.2021.315.285) (KAR id:77048) [link](https://kar.kent.ac.uk/77048/11/Roitzheim%20published%20version.pdf)
2. Blumberg, Andrew J., and Michael A. Hill. "Operadic multiplications in equivariant spectra, norms, and transfers." Advances in Mathematics 285 (2015): 658-708. [link](https://pdf.sciencedirectassets.com/272585/1-s2.0-S0001870815X00144/1-s2.0-S000187081500256X/main.pdf?X-Amz-Security-Token=IQoJb3JpZ2luX2VjEIL%2F%2F%2F%2F%2F%2F%2F%2F%2F%2FwEaCXVzLWVhc3QtMSJHMEUCIQCO6vfKKcndrwlTgCHNSbiJ2G8VCUH%2FilkcfjXDXcyxTgIgZtDHloTThyJm1sH04X9w7nLaUBSaNozzN2P5W8cezasquwUI2%2F%2F%2F%2F%2F%2F%2F%2F%2F%2F%2FARAFGgwwNTkwMDM1NDY4NjUiDCT15dfFZPANtwdJuiqPBTyJy7Ib9n2n6I1jiycZo62hL01bwagymcPU1U5wh4Fsp6qRYZQewL3jJCPhUwiqbHKpvQ7deLPLDZuMsIfHPbegRL%2F1IOh7egNBX3lwbO8bDBkMdbgjWRecwQMpKIQV3XXZPe4nnK5BD50BkRpw2opoE3GNN%2FelGr6OYde4HT4P%2F730lgzfQyf8JlyPow8HEU4vvoph1T9iw6c346bwIdWZ%2FT%2Fcj8DEGfAXTdHI1c%2Bkd80q6Dx4i1wDWblQFRZrRU921OgPvLUF3uTONERuN85maW%2F7DdgQ3Zip3l3CXYf9cCCKNW%2B7fvHionqKcCmYGbx8p%2Ff2PzKGVssrfqZJ7MX9OZlOWpbJxrXLRNXq%2BrOZAES%2F1SafzrSagVXiI3zYMqoLTDcTjkQi6cacwGNjErZNocPbpSViguC%2FwXJAXMnOILw1BWsvTHsUgYrhspqapslU9yVhCU57dTgOHYeuS4%2BQAgc0qq%2BBAZbKrxTKP%2B08z6GT2CdAU4aJrtH6SVAvwAtqgMNoSn7MCx%2B1mQZ1wjMTMXwG3h5HfQcUT3%2BdsK6UHfiTKKKrHZrwRyUrUTN3V8ocGybVFA3iOAoMi8lWAzpYWbOXdl3ys7nDdw%2BK%2BuISeivXEzSQiQ09u7emrDA0G%2BFaAI9cOfy8vdW6QUn0jbNHrYjDpc%2BTbUoRsXjQPfs33%2FHoBNwDK03tyUkiNbYTQyskE%2FyABbmkRaSKyNx12BX8EnJic1lk6FClJy0XtBluKnqEUsF4QxSbHoyYmxL9IsYCPjwtATsL7M4eERN8XMDCF4SoAxQHCgDcKNrUnnQ3mlug5tH6jC2%2BuZzRA%2Flf8Oy6rnooeLgkCMalB%2FZYRY%2FpNV1uQfamWXuvndfbQn4wqJnSpAY6sQFMkNuESlJQl3AjJPupNwtns3qtMYKW96tb%2FWNJ4GT5RAPrH1qSVgO%2BtI%2Bvz5TmwcBPYqtOCJLMpa0cqjtbeGaTTRDnwPui7DBwWCJGJ5Qor%2ByIVbEhsaahQdGtAq6rWdQnT1Tlt6X51984kibwuU98VVPsCip9l1JNgAcDR7eM8KNcdikU3Xw9h3tVdu3J3OlXdlPE3rl%2B34WDdrtWicA%2FcKqOl2ySqo0PtMrVvtMjQRI%3D&X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Date=20230622T185116Z&X-Amz-SignedHeaders=host&X-Amz-Expires=299&X-Amz-Credential=ASIAQ3PHCVTYR47UNKXY%2F20230622%2Fus-east-1%2Fs3%2Faws4_request&X-Amz-Signature=c18e3dea7a3496c3ff156ac0be1a78f3c0444ce307595dbf4d1e548b14d38e1e&hash=d24d35890bdfe424228276c45f5dc1c2c3b21a3f7ce2c71da852cab1813cc034&host=68042c943591013ac2b2430a89b270f6af2c76d8dfd086a07176afe7c76c2c61&pii=S000187081500256X&tid=spdf-400ca13a-e793-461d-b061-5aac41cb1648&sid=92a107798e6f5344926abbd44f81c8e93754gxrqb&type=client&tsoh=d3d3LnNjaWVuY2VkaXJlY3QuY29t&ua=0c08520b065400005950&rr=7db6ae823d979a72&cc=in)